Click here to read the original article.
What is game theory?
Game theory describes a situation in which a finite number of players analyze not only his or her own decisions, but also the decisions of the other players, before acting in a way that optimizes his or her utility.
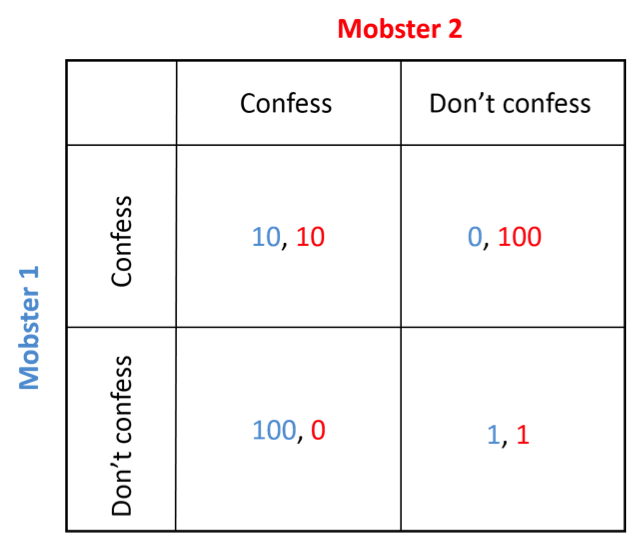
Take the most famous example of game theory, the Prisoner’s Dilemma. In this scenario, two mobsters are held in separate cells, each one being interrogated by a policeman. They are both given the same deal. If both of them confess to the murder individually, they each get ten years in prison. If one of them confesses, then he gets to go free while the other one is imprisoned for life. If neither of them confesses, they both spend a year in jail.
The decision diagram is shown below:
A game theory scenario must satisfy a few conditions:
- There are a finite number of players who face a finite number of decisions;
- Players are rational, i.e. they will do what is best for them;
- Players cannot collaborate to settle on the best outcome.
Nash Equilibrium
The Nash equilibrium describes which scenario the players will settle at. Let us consider the Prisoner’s Dilemma again.
Take Mobster 1. If Mobster 2 confesses, it is better for Mobster 1 to confess rather than not confess, as the former will get him only 10 years in prison while the latter lands him a lifetime. If Mobster 2 does not confess, it is better for Mobster 1 to confess rather than not confess, as the former will let him avoid jail entirely while the latter means he is in jail for a year. Thus, whatever Mobster 2 decides to do, it is in Mobster 1’s best interest to confess.
If we take Mobster 2 now, the reasoning is exactly the same, and it is in Mobster 2’s best interest to confess.
Thus, both mobsters will confess and they will each spend 10 years in prison.
Despite the fact that if they had both not confessed, they would each have received a much lighter sentence, they both did what was best for themselves individually. Herein lies the importance of the Nash equilibrium: the optimal action of an individual does not optimize utility in a society.
Dominant, dominated, and mixed strategies
For only a single Nash equilibrium to exist, there must be either a dominant or a dominated strategy.
A dominant strategy is one where regardless of what the other player decides to do, a certain action is always better for a player. For example, regardless of what Mobster 2 decided to do, it is always in Mobster 1’s best interest to confess.
A dominated strategy is the exact opposite: regardless of what the other player decides to do, a certain action is always worse for a player. In the Prisoner’s Dilemma scenario, not confessing is always worse for Mobster 1.
It is important to note the distinction between a dominant and a dominated strategy. In a two-player game, if there is a clear dominant strategy, then the opposite decision is the clear dominated strategy. However, once a game expands past two players, a dominated strategy might be clear while a dominant strategy is not.
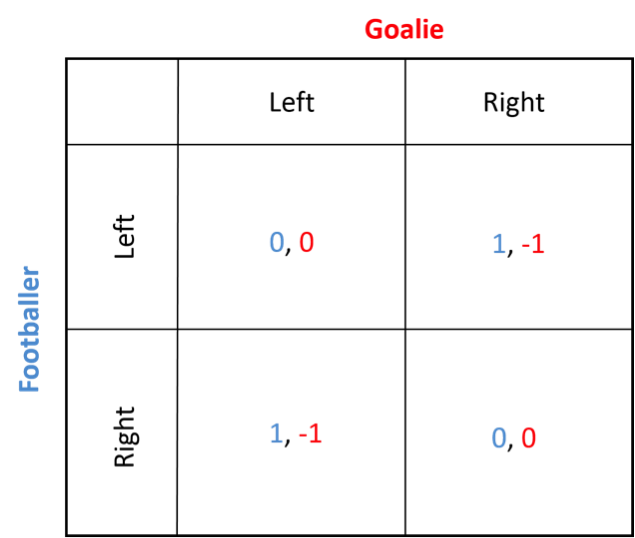
Some games have neither a dominant nor a dominated strategy. These games are called mixed strategy games. Take, for example, a game of football. A footballer who is about to score a goal faces a goalie, who tries to prevent a goal from being scored. This is shown in the decision diagram below.
Similarly, for the goalie, if the footballer kicks left, the goalie should also dive left. If the footballer kicks right, the goalie should dive right. There is no dominant strategy here.
Resultantly, there is no single Nash equilibrium. Instead, we find two Nash equilibria, depending on the decisions each player takes.
Game theory in the real world – Braess’ Paradox
Let us consider a real-world example of game theory: the construction of a highway in a transport system.
Braess’ Paradox holds that, counterintuitively, adding a highway to a transport system will increase travel time for an individual. To read about Braess’ paradox in full, click here. I will be outlining the basics of the paradox.
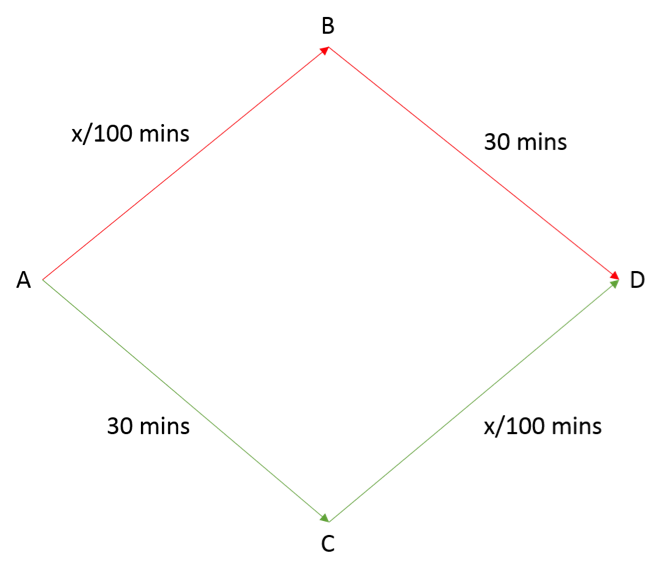
Assume 4000 vehicles using the transport system. The Nash equilibrium is that 2000 vehicles would go through route B while 2000 go through route C. Why is this the Nash equilibrium?
Assume 3000 cars go through route B; consequently, there are 1000 cars travelling through route C. It takes people on route B [(3000/100)+30]=60 minutes to get to point D. It takes people on route C [(1000/100)+30]=40 minutes to get to point D. Thus, people on route B will switch over to route C to reduce traveling time.
Recall that the Nash equilibrium is when an individual does not want to change their choice of action, as they have nothing to gain from doing so. This will only happen when travel time between the two routes is equal, i.e. when there is an equal amount of traffic on either route. Thus, there will be 2000 vehicles on either route, and it would take them 50 minutes to reach point D.
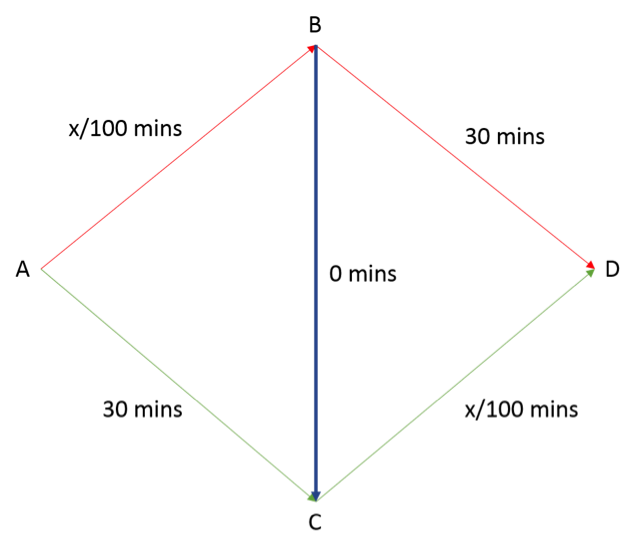
Now, assume a highway has been added between point C and D, as illustrated below:
A to B, B to C, and then C to D, or A to C, C to B and then B to D.
Let’s consider the former with 1000 vehicles. It would take everyone [(4000/100)+0+(4000/100)]=80 minutes to get to point D.
For the latter case, it takes [30+0+30]=60 minutes to get to point D. Thus, individuals will choose to travel from A to C to B to D.
Now, some vehicles will choose to take the first path, while others take the second. The Nash equilibrium will be when the time travelled in both paths is equal, i.e. it takes 60 minutes to travel by either path.
This will happen when there are 300 vehicles on the first path. Note, however, that the use of the highway has increased travel times for all individuals by 10 minutes.
Why the Nash equilibrium matters
The Nash equilibrium assumes many things, including rational behavior and an ability to successfully predict a player’s payoffs. The biggest thing it assumes, however, is perfect information. In other words, a player knows exactly how another player will act given any scenario in the game. This, of course, is not the case in reality.
The Nash equilibrium has been adjusted by many others since John Nash himself. One revision includes uncertainty about people’s payoffs. Another includes the knowledge of non-credible threats, i.e. knowing whether another player will actually act in a certain way or whether he is just claiming that he will.
Despite all its flaws, the Nash equilibrium is one of the more revolutionary findings in economics for a few reasons. Firstly, the Nash equilibrium shows that individuals do not just weigh their own costs to maximize utility – they look at other players in the market to do so as well. Secondly, it shows that a utility maximizing individual does not necessarily maximize utility for a society. In perfectly competitive markets, for example, an individual’s choice of selling their product for the price at which it costs to produce it maximizes utility not only for the seller, but for the collective market as well.
The third way in which the Nash equilibrium is important is through the lens of government policy. Take a game theory scenario in which the dominant strategy for an oil company is to pollute a river. Taxation, or other methods of decreasing the payoff, shifts the company’s dominant strategy to not polluting at all. In this way, the Nash equilibrium is another way to view equilibrium analysis.
 RSS Feed
RSS Feed
